【课标要求】
| 考点 | 课标要求 | 知识与技能目标 |
| 了解 | 理解 | 掌握 | 灵活应用 |
| 三角形 | 画出任意三角形的角平分线、中线和高 | | ∨ | | |
| 全等三角形的概念 |
| 三角形全等的条件 | ∨ | | | |
| 三角形的中位线 | | | ∨ | |
| 等腰三角形、直角三角形、等边三角形的概念 | | | ∨ | |
【知识梳理】
①了解三角形有关概念(内角、外角、中线、高、角平分线),会画出任意三角形的角平分线、中线和高.了解三角形的稳定性。三角形两边之和大于第三边。
②探索并掌握三角形中位线的性质。
【能力训练】
一、选择题:
1.如图,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( ).
(A)全部正确 (B)仅①正确 (C)仅①、②正确 (D)仅①、③正确
2.已知线段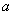 、
、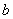 ,要想作一条线段AB,使AB=
,要想作一条线段AB,使AB=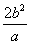 ,正确的作法是(图中直线m∥n)( ).
,正确的作法是(图中直线m∥n)( ).
3.将下列命题的条件与结论互换,得到的命题仍是真命题的是( ).
(A)对顶角相等 (B)全等三角形的对应角相等
(C)直角三角形两锐角互余 (D)如果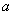 >
>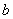 ,
,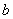 >
>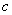 ,那么
,那么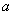 >
>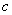
4.如图,将直角边AC=6cm,BC=8cm的直角△ABC纸片折叠,使点B与点A重合,折痕为DE,则CD等于( )
(A)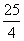 (B)
(B) 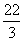 (C)
(C) 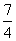 (D)
(D) 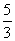
5.如图,结合图形作出了如下判断或推理:
①如图甲,CD⊥AB,D为垂足,那么点C到AB的距离等于C、D两点间的距离;
②如图乙,如果AB∥CD,那么∠B=∠D;
③如图丙,如果∠ACD=∠CAB,那么AD∥BC;
④如图丁,如果∠1=∠2,∠D=120°,那么∠BCD=60°.其中正确的个数是( )个.
(A)1 (B)2 (C)3 (D)4
6.如图,BE、CF是ABC的高,M是BC的中点,则图中三角形一定是等腰三角形的有( )
(A)2个 (B)3个 (C)4个 (D)5个
7.如图,AD、BE是△ABC的高,相交于F点,则图中共有相似三角形( )
(A)6对 (B)5对 (C)4对 (D)3对
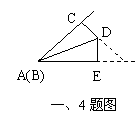
8.如图,在ABG中,D、E和C、F分别是AG、BG的三等分点下面给出四个结论:
(1)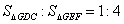 (2)
(2)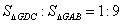
(3)S△EGF:S△GAB=2:3 (4)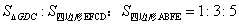
其中结论正确的个数是( )
(A)1 (B)2 (C)3 (D)4
二、填空题
1.如图,将一副三角板叠放在一起,使直角顶点重合于点O,则∠AOC+∠DOB的度数为 度.
2.如图,在△ABC中,∠C=90°,AD是△ABC中∠CAB的角平分线,DE⊥AB于E,要使△ADC≌△BDE,需要添加一个条件,这个条件是 .
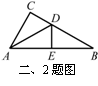
3.一个钢筋三角架,三边长分别为2m、5m、6m,现要求做一个与之相似的钢筋三角架,现只有长为3m和5m的两根钢筋,要求以其中一根为—边,从另根—上截下两段(允许有余料)作为另两边,则另两边的长为 .
4.如图,已知A,B,C,D,E五点的坐标分别为(1,2),(3,2),(4,3),(2,6),(3,5).如果点F在第—象限内,且以D,E,F为顶点的三角形与△ABC全等,那么点F的坐标为 .
5.在一单位为1cm的方格纸上,依右图所示的规律,设定点A1、A2、A3、A4…、An,连结点A1、A2、A3组成三角形,记为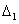 ,连结点A2、A3、A4组成三角形,记为
,连结点A2、A3、A4组成三角形,记为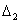 …,连结点An、An+1、An+2组成三角形,记为
…,连结点An、An+1、An+2组成三角形,记为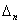 (n为正整数).请你推断,当
(n为正整数).请你推断,当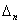 的面积为100cm2时,n= .
的面积为100cm2时,n= .
三、解答题
1.在如图所示的方格纸中,画出,△DEF和△DEG(F、G不能重合),使得△ABC≌△DEF≌DEG.你能说明它们为什么全等吗?
2.如图,有一湖泊,岸边A、B间的距离不能直接测量,为得到A、B间的距离,请你利用测角仪和皮量尺,在岸上设计出两种测量方案(分别画出说明方案的图形,方案的依据需是本单元的有关知识),并就方案写出表示A、B间的距离的所要测量的线段.(经测量所得线段长用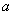 (或
(或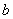 或
或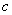 等)表示,角度用α(或β)表示).
等)表示,角度用α(或β)表示).
3.测量小玻璃管口径的量具CDE上,CD=l0mm,DE=80mm.如果小管口径AB正对着量具上的50mm刻度,那么小管口径AB的长是多少?
4.如图,正方形网格中的小正方形的面积都为1,网格中有△ABC和△DFE.
(1)这两个三角形相似吗?说出你的理由;
(2)请你以网格中的格点为顶点,在网格中再画出一个面积为4且与△ABC相似的三角形.
5.如图,已知,△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=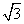 ,BC=1.连结BF,分别交AC、DC、DE于点P、Q、R.
,BC=1.连结BF,分别交AC、DC、DE于点P、Q、R.
(1)△BFG与△FEG相似吗?为什么?
(2)写出图中所有与△ABP相似的三角形(不必证明).
6.如图(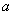 )所示,锐角△ABC中,BC>AB>AC,D、E分别是BC、AB上的动点,连结AD、DE.
)所示,锐角△ABC中,BC>AB>AC,D、E分别是BC、AB上的动点,连结AD、DE.
(1)当D、E运动时,分别在其余的三个图中画出D、E运动的位置;在图(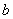 )中画出仅有一组三角形相似的图形;在图(
)中画出仅有一组三角形相似的图形;在图(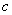 )中画出仅有二组三角形相似的图形;在图(
)中画出仅有二组三角形相似的图形;在图(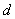 )中画出有三组三角形相似的图形.
)中画出有三组三角形相似的图形.
(2)BC=9,AB=8,AC=6,就图(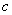 )求出DE的长.
)求出DE的长.
7.在直角坐标系中,已知A(-4,0)、B(1,0)、C(0,-2)三点.请按以下要求设计两种方案:作一条与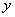 轴不重合,与△ABC的两边相交的直线,使截得的三角形与△ABC相似,并且面积是△AOC面积的
轴不重合,与△ABC的两边相交的直线,使截得的三角形与△ABC相似,并且面积是△AOC面积的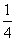 .分别在下面的两个坐标中系画出设计图形,并写出截得的三角形三个顶点的坐标.
.分别在下面的两个坐标中系画出设计图形,并写出截得的三角形三个顶点的坐标.
8.(1)已知:如图①,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连结FG,延长AF、AG,与直线BC相交.求证:FG=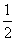 (AB+BC+AC).
(AB+BC+AC).
(2)若BD、CE分别是△ABC的内角平分线,其余条件不变(如图②),线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想,并给予证明.
参考答案:
一、选择题:1-4:ACCD;5—8:BDBC
二、填空题:1.180;2.∠B=30度;3.1,2.5;4.(2,8);5.10
三、解答题:
1.略;2.略;3.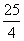 ;4.相似;5.相似,利用数值的比证明;6.略;7.略;8.提示:延长AG、AF相交于BC的延长线与反向延长线于点M、N,利用中位线证明。
;4.相似;5.相似,利用数值的比证明;6.略;7.略;8.提示:延长AG、AF相交于BC的延长线与反向延长线于点M、N,利用中位线证明。

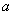 、
、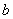 ,要想作一条线段AB,使AB=
,要想作一条线段AB,使AB=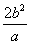 ,正确的作法是(图中直线m∥n)( ).
,正确的作法是(图中直线m∥n)( ).
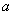 >
>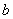 ,
,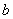 >
>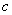 ,那么
,那么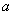 >
>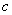
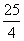 (B)
(B) 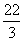 (C)
(C) 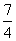 (D)
(D) 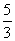




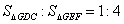 (2)
(2)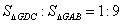
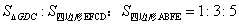




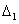 ,连结点A2、A3、A4组成三角形,记为
,连结点A2、A3、A4组成三角形,记为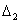 …,连结点An、An+1、An+2组成三角形,记为
…,连结点An、An+1、An+2组成三角形,记为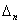 (n为正整数).请你推断,当
(n为正整数).请你推断,当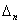 的面积为100cm2时,n= .
的面积为100cm2时,n= .

![]() (或
(或![]() 或
或![]() 等)表示,角度用α(或β)表示).
等)表示,角度用α(或β)表示).


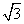 ,BC=1.连结BF,分别交AC、DC、DE于点P、Q、R.
,BC=1.连结BF,分别交AC、DC、DE于点P、Q、R.
![]() )所示,锐角△ABC中,BC>AB>AC,D、E分别是BC、AB上的动点,连结AD、DE.
)所示,锐角△ABC中,BC>AB>AC,D、E分别是BC、AB上的动点,连结AD、DE.![]() )中画出仅有一组三角形相似的图形;在图(
)中画出仅有一组三角形相似的图形;在图(![]() )中画出仅有二组三角形相似的图形;在图(
)中画出仅有二组三角形相似的图形;在图(![]() )中画出有三组三角形相似的图形.
)中画出有三组三角形相似的图形.![]() )求出DE的长.
)求出DE的长.
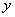 轴不重合,与△ABC的两边相交的直线,使截得的三角形与△ABC相似,并且面积是△AOC面积的
轴不重合,与△ABC的两边相交的直线,使截得的三角形与△ABC相似,并且面积是△AOC面积的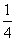 .分别在下面的两个坐标中系画出设计图形,并写出截得的三角形三个顶点的坐标.
.分别在下面的两个坐标中系画出设计图形,并写出截得的三角形三个顶点的坐标.
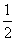 (AB+BC+AC).
(AB+BC+AC).

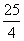 ;4.相似;5.相似,利用数值的比证明;6.略;7.略;8.提示:延长AG、AF相交于BC的延长线与反向延长线于点M、N,利用中位线证明。
;4.相似;5.相似,利用数值的比证明;6.略;7.略;8.提示:延长AG、AF相交于BC的延长线与反向延长线于点M、N,利用中位线证明。