行测容斥问题作为常考题型之一,国考考试在即重点备考没有错,下面由留学群小编为你精心准备了“2021公务员行测数量关系备考:容斥问题”,持续关注本站将可以持续获取更多的考试资讯!
2021公务员行测数量关系备考:容斥问题
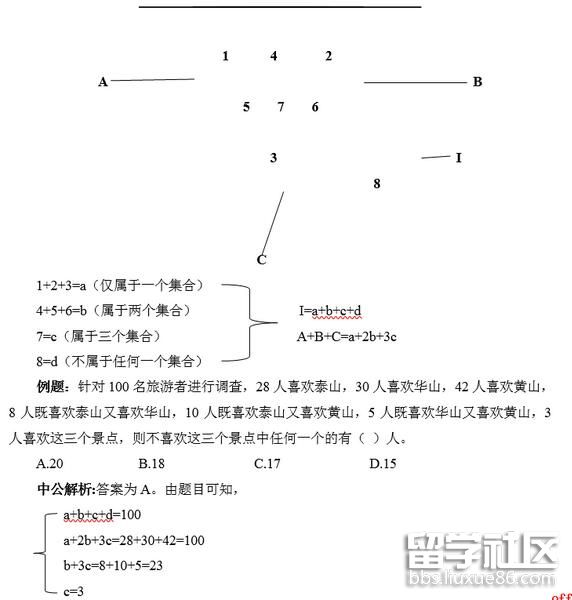
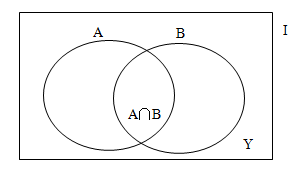
首先,了解基础公式,两者容斥的公式是: I=A+B—X+Y。
【例1】某大学年度奖学金评定中,某专业1班的学生中获得优秀学生奖学金的人数为6人,获得进步奖学金的人数为8人,两种奖学金都没有获得的人数为16人,已知该班级有29人,那么,两种奖学金都获得的人数为( )。
A.1 B.0 C.2 D.3
【解析】A。该班获得奖学金的有29-16=13人,则所求为6+8-13=1人。
【例2】学校举办跳绳比赛,其中包括速度和花式两类,某班报名参加速度类比赛有26人,报名参加花式类比赛的有15人,其中有5个同学两类比赛都参加了,其余9名未参加比赛的同学组成了班级的拉拉队,问全班一共有( )学生。
A.35 B.30 C.50 D.45
【解析】D。两者容斥求和=26+15-5+9=45人。
【例3】电视台向100人调查昨天收看电视情况,有62人看过2频道,有34人看过8频道,有11人两个频道都看过。问,两个频道都没有看过的有多少人?
A.4 B.15 C.17 D.18
【解析】B。设A=看过2频道的人(62),B=看过8频道的人(34),则A+B=62+34=96;A∩B=两个频道都看过的人(11);根据公式A∪B=A+B-A∩B=96-11=85,所以,两个频道都没有看过的人数为100-85=15人。
接下来,学习三者容斥公式
公式一:I=A+B+C-A∩B-B∩C-A∩C+X+Y
公式二:I=A+B+C—b—2X+Y
【例4】某外国的考察组来到我公司进行考察访问。这个考察组共有28人组成,他们中,14人会说英语,12人会说韩语,10人会说日语。既会说英语又会说韩语的有8人,既会说英语又会说日语的有6人,既会说韩语又会说日语的有4人,而且这个考察组中还有2人能同时说出这三种语言。请问,这个考察组中,对这三种语言而言,只会说一种语言的人比一种语言都不会说的人少( )人。
A.2 B.4 C.6 D.8
【解析】A。会至少一种语言的为14+12+10-(8+6+4)+2=20人,则一种语言都不会的有28-20=8(人)。只会英语的有14-(8+6-2)=2(人);只会韩语的有12-(8+4-2)=2(人);只会日语的有10-(6+4-2)=2(人),则只会一种语言的有2+2+2=6(人),比一种语言都不会的少2人。
行测言语理解与表达备考:选词填空答题技巧
在行测考试中,言语理解题目本是大家非常自信的题目,因为被数量资料的数学难倒那是不会,被逻辑难住那是逻辑思维不强,被言语难倒那说不过去,可是偏偏言语的真香定律把大家搞的哭笑不得。
今天小编先带大家来看看在言语选词填空题目中的真香定律有哪些呢?真香定...